「量子情報の新展開」(NHQIS)における研究成果の発表
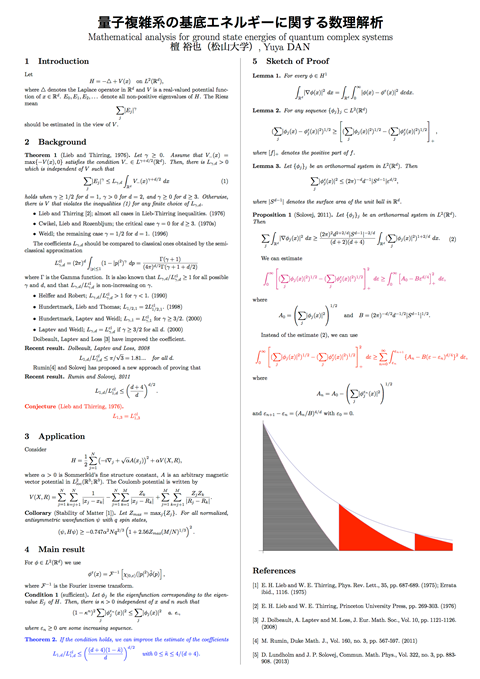
2014年3月22日(日曜)~25日(水曜)、京都大学基礎物理学研究所で開催された研究会「量子情報の新展開」において、量子複雑系の基底状態エネルギーに関する最新の研究成果「量子複雑系の基底エネルギーに関する数理解析」をポスターによって発表しました。 なお、今回の発表では、KEKでの発表に数学的証明を加えました。
概要
Schrödinger作用素に対する負の固有値について、LiebとThirringらを中心に証明が完成したLieb-Thirring不等式が成り立つ。特に、3次元以上の1次モーメントを考える場合には、その不等式の係数が準古典近似によって得られる理想値に一致するという予想がある。現時点では、その予想は肯定的(数学的証明)にも否定的(反例の提示)にも決着がついていないが、Dolbeault、LaptevおよびLossによって2008年に示された係数の精緻化が最善の成果であり、Lieb-Thirring予想の解決に向けて証明の試みに挑戦されている。一方、2011年に全く異なるアプローチを提案したRuminの手法に沿ってSolovejらがLieb-Thirring予想の解決を目指している。本研究は、Rumin-Solovejの手法を基盤としてLieb-Thirring不等式の精緻化およびLieb-Thirring予想の十分条件を提案するものである。
- E. H. Lieb and W. E. Thirring, "Bound for the Kinetic Energy of Fermions which Proves the Stability of Matter," Phys. Rev. Lett., 35, 687–689. (1975); Errata ibid., 1116. (1975)
- E. H. Lieb and W. E. Thirring, "Inequalities for the Moments of the Eigenvalues of the Schrödinger Hamiltonian and their Relation to Sobolev Inequarities," in Studies in Mathematical Physics, edited by E. Lieb, B. Simon and A. Wightman Princeton University Press, Princeton, NJ, pp. 269–303. (1976)
- J. Dolbeault, A. Laptev and M. Loss; "Lieb-Thirring inequalities with improved constants," J. Eur. Math. Soc., Vol. 10, pp. 1121-1126. (2008)
- M. Rumin, "Balanced distribution-energy inequalities and related entropy bounds," Duke Math. J., Vol. 160, no. 3, pp. 567–597. (2011)
- D. Lundholm and J. P. Solovej, "Hardy and Lieb-Thirring inequalities for anyons," Commun. Math. Phys. Vol. 322, no. 3, pp. 883–908. (2013)
発表ポスター